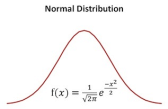
Normally distributed curve formula

Post

Posted
Rating:
#1 (In Topic #93)
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
Hi there!

Are any of you good with maths? Just for fun, I wanted to make a function that accelerates and breaks a span of values according to a normally distributed bell curve.

Image

Bell Curve

Bell Curve

(Click to enlarge)


Code (gambas)

  1. Public Sub Go_Click()
  4.  
  5.  h = BellCurve(0.0, 1, 0.01)
  6.  
  7.  For Each f In h
  8.    Print f
  10.  
  12.  
  13. Public Sub BellCurve(Val1 As Float, Val2 As Float, Dist As Float) As Float[]
  14.  
  15.   Dim i, y As Float
  16.   Dim fValues As New Float[]
  17.  
  18.   For i = Val1 To Val2 Step Dist
  19.     y = (1 / Sqr(2 * Pi)) * (Exp((- Exp2(i)) / 2))
  20.     fValues.Add(y)
  21.   Next
  22.  
  23.   Return fValues
  24.  
  26.  

I think I made the formula according to the picture, but the values given does not make sense.

Code

0,24197072451914
0,24113066638911
0,24028771212673
0,23944187227953
0,23859315771476
0,23774157962215
0,23688714951667
0,23602987924122
0,23516978096936
0,23430686720801
0,23344115080014
0,23257264492739
0,23170136311274
0,23082731922316
0,22995052747215
0,22907100242238
0,22818875898819
0,22730381243817
0,22641617839766
0,22552587285122
0,22463291214508
0,22373731298958
0,22283909246157
0,22193826800677
0,22103485744211
0,220128878958
0,21922035112066
0,21830929287431
0,21739572354336
0,2164796628346
0,21556113083929
0,21464014803524
0,21371673528889
0,21279091385723
0,21186270538981
0,21093213193062
0,20999921591996
0,20906398019621
0,20812644799763
0,20718664296407
0,20624458913857
0,20530031096903
0,20435383330971
0,20340518142271
0,20245438097945
0,201501458062
0,20054643916439
0,19958935119386
0,19863022147206
0,19766907773612
0,19670594813977
0,19574086125423
0,19477384606918
0,1938049319936
0,19283414885647
0,19186152690755
0,19088709681789
0,18991088968045
0,18893293701048
0,18795327074596
0,18697192324783
0,18598892730022
0,18500431611055
0,18401812330958
0,18303038295134
0,18204112951297
0,18105039789446
0,18005822341836
0,17906464182929
0,17806968929343
0,17707340239787
0,17607581814992
0,17507697397621
0,17407690772178
0,17307565764904
0,1720732624366
0,17106976117802
0,1700651933804
0,16905959896292
0,16805301825526
0,16704549199583
0,16603706132997
0,16502776780798
0,16401765338308
0,16300676040915
0,1619951316385
0,16098281021934
0,15996983969327
0,15895626399256
0,15794212743733
0,15692747473258
0,15591235096512
0,15489680160036
0,1538808724789
0,15286460981311
0,15184806018344
0,15083127053468
0,14981428817206
0,14879716075719
0,14777993630387
Online now: No Back to the top

Post

Posted
Rating:
#2
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
I want to achieve the effect seen on the lines and circles here.

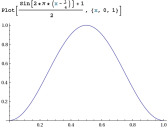
Eventually, I also want to understand the bouncing effect seen on the middle circle.
Online now: No Back to the top

Post

Posted
Rating:
#3
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
This one worked :)

Code

y = (Sin(2 * Pi * (i - (1 / 4))) + 1) / 2

Image

(Click to enlarge)

Online now: No Back to the top

Post

Posted
Rating:
#4
cogier
Avatar
Guru
cogier is in the usergroup ‘Guru’
Regarding the lines, see the attached. I'll have a go at the circles later.
Attachment
Online now: No Back to the top

Post

Posted
Rating:
#5
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
Thanks cogier :)

I think you misunderstood my question a tad. I want the bars to accelerate, and then brake at the end - gracefully. After that I want to add a feature making them to bounce once they've hit the "wall".

For the acceleration/braking down I want to determine the speed using a bell curve (which will in the end determine the delay between each increment/decrement in the value of the progress bar). I have already made a gauge component for the circle, so I only need the correct equation. The last one works sort of, but it is not optimal. I need it more flat in the ends, and more pointy in the middle. Working on what part of the equation that takes care of that  :ugeek:

I am playing around with KmPlot to see how the different curves looks like.
Online now: No Back to the top

Post

Posted
Rating:
#6
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
This is the current progress:

Attachment

I need something better than a sinus curve though :)
Online now: No Back to the top

Post

Posted
Rating:
#7
cogier
Avatar
Guru
cogier is in the usergroup ‘Guru’
I have tried your solution but it seems very complicated. Have a look at the attached for a different solution, but still using the Bell Curve principle.

Attachment
Online now: No Back to the top

Post

Posted
Rating:
#8
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
Thanks again cogier, but I really want to use the bell curve approach, for several reasons:

It is fun and satisfying
It takes less code
It can be altered with ease, for example the acceleration can be adjusted by a single variable,

It is not all that complex, but I just haven't had time to find the correct formula for my usage. I will eventually ask some of my friends who are heavily educated in maths :)
Online now: No Back to the top

Post

Posted
Rating:
#9
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
I forgot to mention here that this was the end result of the challenge: Gambas One - Gambas ONE

Had some help of a friend with a PhD :)
Online now: No Back to the top

Post

Posted
Rating:
#10
Cedron
Avatar
Regular
Cedron is in the usergroup ‘Regular’
This is old, but I don't know if you ever figured it out.  You had a simple mistake in your formula.  Coincidentally, I put a bell curve in my second interpolation project.

Gambas One - Gambas ONE

No Phd, but a BS in Mathematics here.

Code (gambas)

  1. Public Sub BellCurve(Val1 As Float, Val2 As Float, Dist As Float) As Float[]
  2.  
  3.   Dim i, y As Float
  4.   Dim fValues As New Float[]
  5.    
  6.   For i = Val1 To Val2 Step Dist
  7.     y = (1 / Sqr(2 * Pi)) * Exp(-i * i / 2)
  8.     fValues.Add(y)
  9.   Next
  10.    
  11.   Return fValues
  12.  
  14.  
.... and carry a big stick!
Online now: No Back to the top

Post

Posted
Rating:
#11
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
Hi Cedron!

Yes, I posted the link to the final solution in my previous post. You can find the project there, and a video showing the results :)

Thanks anyways!
Online now: No Back to the top

Post

Posted
Rating:
#12
jornmo
Avatar
Regular
jornmo is in the usergroup ‘Regular’
Btw. BS in Maths sounds great! I have a BS in economics, which has some maths and statistics in it :)
Online now: No Back to the top

Post

Posted
Rating:
#13
Cedron
Avatar
Regular
Cedron is in the usergroup ‘Regular’
 The thing about math is that it really really works.  It's sort of immune to obsolescence which is also nice.

You might get a kick (or some ideas) out of the programs I posted in my Interpolation Methods thread.  I would really appreciate it if you could download the FFTW-0.0.3.tar.gz, run the program and tell me if it runs.  If it does, you should find a "libGambas_FFTW.so" file in your project directory.

It is required for the first program.  Cogier got it working with the old version, but had to work too hard to get it done.  This one is supposed to be easier.

The first program needs the library, the second doesn't, it should work straight up.

Thanks,
Ced
.... and carry a big stick!
Online now: No Back to the top
1 guest and 0 members have just viewed this.